小咸鱼
0%

C#容器源码之Queue

发表于 更新于 分类于

前言

复习下Queue的一些知识点。

源码地址。

正文

定义

队列, 先进先出(FIFO)的顺序容器, 底层为数组。

成员变量

修饰符 类型 变量名 作用简述
private 泛型数组 _array 队列数组数据
private int _head 队首下标位置
private int _tail 队尾下标位置
private int _size 队列元素数量
private int _version 迭代时用于数据版本校验
private Object _syncRoot 多线程下的同步对象，已弃用，多线程建议使用ConcurrentQueue
private static 泛型数组 _emptyArray 默认构造函数初始化后指向的空数组

构造函数

三种构造函数:

  1. 默认构造函数，初始化数组数据为只读的空数组，下一次Enqueue就会触发扩容
    1
    2
    3
    public Queue() {
        _array = _emptyArray;            
    }
  2. 预分配大小的构造函数
1
2
3
4
5
6
7
8
9
public Queue(int capacity) {
    if (capacity < 0)
        ThrowHelper.ThrowArgumentOutOfRangeException(ExceptionArgument.capacity, ExceptionResource.ArgumentOutOfRange_NeedNonNegNumRequired);
    
    _array = new T[capacity];
    _head = 0;
    _tail = 0;
    _size = 0;
}
  1. 用其他容器初始化的构造函数，可能会触发多次扩容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public Queue(IEnumerable<T> collection)
{
    if (collection == null)
        ThrowHelper.ThrowArgumentNullException(ExceptionArgument.collection);
 
    _array = new T[_DefaultCapacity];
    _size = 0;
    _version = 0;
 
    using(IEnumerator<T> en = collection.GetEnumerator()) {
        while(en.MoveNext()) {
            Enqueue(en.Current);
        }
    }            
}

扩容机制

以当前队列元素数量2倍的容量来扩容，如果容器初始容量小于4， 那么会再额外分配最小容量为4的空间， 代码如下

1
2
3
4
5
6
7
8
if (_size == _array.Length) {
    int newcapacity = (int)((long)_array.Length * (long)_GrowFactor / 100);
    if (newcapacity < _array.Length + _MinimumGrow) {
        newcapacity = _array.Length + _MinimumGrow;
    }
    SetCapacity(newcapacity);
}

重新分配数组内存，然后将旧数据拷贝过去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
 private void SetCapacity(int capacity) {
    T[] newarray = new T[capacity];
    if (_size > 0) {
        if (_head < _tail) {
            Array.Copy(_array, _head, newarray, 0, _size);
        } else {
            Array.Copy(_array, _head, newarray, 0, _array.Length - _head);
            Array.Copy(_array, 0, newarray, _array.Length - _head, _tail);
        }
    }
    
    _array = newarray;
    _head = 0;
    _tail = (_size == capacity) ? 0 : _size;
    _version++;
}

注意这里存在队首索引在队尾索引之后的情况(_head >= _tail)，这是因为队列的逻辑结构是一个环形结构，后文会详细说明。

关键函数

Enqueue

将一个元素添加到队列尾部, 因为是环形结构，_tail的索引需要模除一下获得实际的下标位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void Enqueue(T item) {
    if (_size == _array.Length) {
        int newcapacity = (int)((long)_array.Length * (long)_GrowFactor / 100);
        if (newcapacity < _array.Length + _MinimumGrow) {
            newcapacity = _array.Length + _MinimumGrow;
        }
        SetCapacity(newcapacity);
    }
    
    _array[_tail] = item;
    _tail = (_tail + 1) % _array.Length;
    _size++;
    _version++;
}

Dequeue

移除并返回队首元素

1
2
3
4
5
6
7
8
9
10
11
public T Dequeue() {
    if (_size == 0)
        ThrowHelper.ThrowInvalidOperationException(ExceptionResource.InvalidOperation_EmptyQueue);
    
    T removed = _array[_head];
    _array[_head] = default(T);
    _head = (_head + 1) % _array.Length;
    _size--;
    _version++;
    return removed;
}

Peek

获取队首元素

1
2
3
4
5
6
public T Peek() {
    if (_size == 0)
        ThrowHelper.ThrowInvalidOperationException(ExceptionResource.InvalidOperation_EmptyQueue);
    
    return _array[_head];
}

Contains

从头到尾遍历判断元素是否在队列内

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public bool Contains(T item) {
     int index = _head;
     int count = _size;
 
     EqualityComparer<T> c = EqualityComparer<T>.Default;
     while (count-- > 0) {
         if (((Object) item) == null) {
             if (((Object) _array[index]) == null)
                 return true;
         } 
         else if (_array[index] != null && c.Equals(_array[index], item)) {
             return true;
         }
         index = (index + 1) % _array.Length;
     }
    
     return false;
 }

环形结构说明

这里举例说明下，假设我们有个队列长度为6的Queue<int>，然后把队列用数字 1~6 塞满。

1
Queue<int> q = new Queue<int>(new[] { 1, 2, 3, 4, 5, 6 });

这时候队列结构如下图。

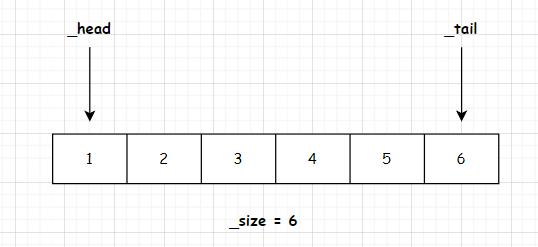
queue1

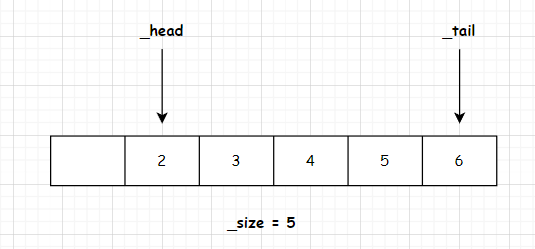
接下来我们调用一次出列

1
q.Dequeue();

变化后的结构如下图

queue2

接着调用一次入列将数字7添加到队尾

1
q.Enqueue(7);

结构如下图

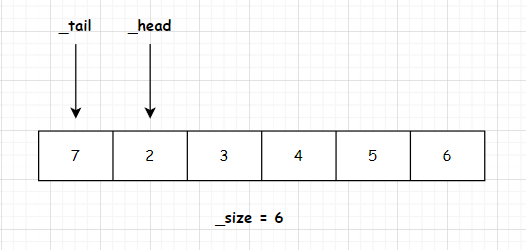
queue3

可以看到当_tail递增到数组末尾时(_tail == 6), 发现_head之前还有剩余空间，那么正好可以复用之前的空间,于是 _tail % 6(数组长度) = 0，正好是数组出队后预留的空位置，那么_tail就直接占用该位置即可。从逻辑结构上来说就好像数组的首尾拼在一起形成了一个顺时针的环状结构。

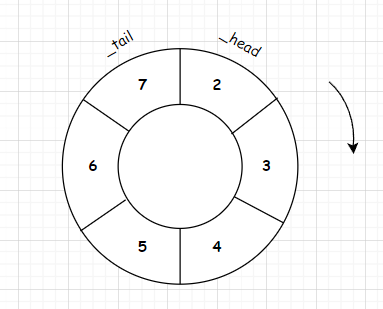
queue4

这样就可以循环复用空间直到队列变满为止(_size == length)。

为什么要使用环形结构?

除了可以复用空间外，还可以反过来思考下，如果逻辑上不使用环形结构会怎么样?
那么_head和_tail会持续递增下去，当达到数组末尾后，如果有新的元素添加到末尾，那么就不得不把当前所有的元素都往前挪，然后更新_head和_tail为新的下标。

即在不使用环形结构的情况下，入队操作可能会导致O(N)时间复杂度的操作，而使用索引来mod数组长度的操作来模拟环形队列，就可以保证在不扩容的情况下每次入队操作都是O(1)。

总结

  1. 调用Peek和Dequeue注意队列是否为空，否则会抛异常。

  2. 预估好容量，降低多次扩容带来的开销。

  3. 该队列不是双端队列Deque，只能操作队首元素，需要操作队末元素的话，考虑换用List或者自己实现。